Data Sheet 60: Pump-Down Time for Vacuum Tanks
When evacuating a tank, the approximate running time of the vacuum pump to reach the desired degree of vacuum can be estimated from this chart, either starting from atmospheric pressure or starting from a lower vacuum and pumping to a higher level.
The chart was calculated for a vacuum pump which could attain a maximum vacuum of 28˝ Hg (when the barometric pressure was 30˝ Hg) when running with inlet plugged (deadheaded). This is typical of small vane or piston type vacuum pumps designed for commercial vacuums. If using a pump with other than 28˝ Hg deadhead capability, the formula given in the text may be used.
The chart shows running time, in minutes, for a vacuum pump which has a free running displacement (both ports open to atmosphere) of 1 SCFM. For pumps with a different displacement the running time must be adjusted by dividing chart values by the pump displacement.
Running time values are approximate because the efficiency will vary between pumps of different manufacture.
Running time on a 1 SCFM vacuum pump for evacuating a tank
| Tank Volume, in Cubic Feet and Gallons | |||||||||||||
| Cu. Ft. | 1 | 1½ | 2¼ | 3½ | 5 | 7½ | 10 | 17½ | 25 | 40 | 55 | 85 | 130 |
| Gallons | 7.5 | 11.2 | 16.8 | 26.2 | 37.4 | 56.1 | 74.8 | 131 | 187 | 300 | 411 | 636 | 972 |
| Vac. ˝Hg | Time, in Minutes, to Evacuate Tank | ||||||||||||
| 5 | 0.20 | 0.29 | 0.44 | 0.69 | 0.98 | 1.5 | 2.0 | 3.4 | 4.9 | 7.9 | 10.8 | 16.7 | 25.5 |
| 6 | 0.24 | 0.36 | 0.54 | 0.84 | 1.2 | 1.8 | 2.4 | 4.2 | 6.0 | 9.7 | 13.3 | 20.5 | 31.4 |
| 7 | 0.29 | 0.43 | 0.65 | 1.0 | 1.4 | 2.2 | 2.9 | 5.0 | 7.2 | 11.5 | 15.8 | 24.4 | 37.4 |
| 8 | 0.34 | 0.50 | 0.76 | 1.2 | 1.7 | 2.5 | 3.4 | 5.9 | 8.4 | 13.5 | 18.5 | 28.6 | 43.7 |
| 9 | 0.39 | 0.58 | 0.87 | 1.4 | 1.9 | 2.9 | 3.9 | 6.8 | 9.7 | 15.5 | 21.3 | 33.0 | 50.4 |
| 10 | 0.44 | 0.66 | 0.99 | 1.5 | 2.2 | 3.3 | 4.4 | 7.7 | 11.1 | 17.7 | 24.3 | 37.6 | 57.5 |
| 11 | 0.49 | 0.74 | 1.1 | 1.7 | 2.5 | 3.7 | 4.9 | 8.6 | 12.3 | 19.7 | 27.1 | 41.9 | 64.1 |
| 12 | 0.56 | 0.84 | 1.3 | 2.0 | 2.8 | 4.2 | 5.6 | 9.8 | 14.0 | 22.4 | 30.8 | 47.6 | 72.7 |
| 13 | 0.62 | 0.94 | 1.4 | 2.2 | 3.1 | 4.7 | 6.2 | 10.9 | 15.6 | 25.0 | 34.3 | 53.1 | 81.2 |
| 14 | 0.69 | 1.0 | 1.6 | 2.4 | 3.5 | 5.2 | 6.9 | 12.1 | 17.3 | 27.7 | 38.1 | 58.9 | 90.1 |
| 15 | 0.77 | 1.2 | 1.7 | 2.7 | 3.8 | 5.8 | 7.7 | 13.4 | 19.2 | 30.7 | 42.2 | 65.2 | 100 |
| 16 | 0.85 | 1.3 | 1.9 | 3.0 | 4.2 | 6.4 | 8.5 | 14.8 | 21.2 | 33.9 | 46.6 | 72.0 | 110 |
| 17 | 0.93 | 1.4 | 2.1 | 3.3 | 4.7 | 7.0 | 9.3 | 16.3 | 23.4 | 37.4 | 51.4 | 79.4 | 121 |
| 18 | 1.0 | 1.5 | 2.3 | 3.6 | 5.1 | 7.1 | 10.3 | 18.0 | 25.7 | 41.2 | 56.6 | 87.5 | 134 |
| 19 | 1.1 | 1.7 | 2.6 | 4.0 | 5.7 | 8.5 | 11.3 | 19.9 | 28.4 | 45.4 | 62.4 | 96.5 | 148 |
| 20 | 1.3 | 1.9 | 2.8 | 4.4 | 6.3 | 9.4 | 12.5 | 21.9 | 31.3 | 50.1 | 68.9 | 106 | 163 |
| 21 | 1.4 | 2.1 | 3.1 | 4.9 | 6.9 | 10.4 | 13.9 | 24.3 | 34.7 | 55.5 | 76.2 | 118 | 180 |
| 22 | 1.5 | 2.3 | 3.5 | 5.4 | 7.7 | 11.6 | 15.4 | 27.0 | 38.5 | 61.6 | 84.7 | 131 | 200 |
| 23 | 1.7 | 2.6 | 3.9 | 6.0 | 8.6 | 12.9 | 17.2 | 30.1 | 43.1 | 68.9 | 94.8 | 146 | 224 |
| 24 | 1.9 | 2.9 | 4.4 | 6.8 | 9.7 | 14.6 | 19.4 | 34.1 | 48.6 | 77.8 | 107 | 165 | 253 |
| 25 | 2.3 | 3.5 | 5.3 | 8.2 | 11.7 | 17.5 | 23.3 | 40.8 | 58.4 | 93.4 | 128 | 198 | 303 |
| 26 | 2.6 | 4.0 | 5.9 | 9.2 | 13.2 | 19.8 | 26.4 | 46.2 | 66.0 | 106 | 145 | 224 | 343 |
| 27 | 3.3 | 5.0 | 7.5 | 11.7 | 16.7 | 25.0 | 33.3 | 58.3 | 83.3 | 133 | 183 | 283 | 433 |
How to Use the Chart
The free running displacement of your pump must be known. This is the physical volume displaced in one minute of running time, expressed in SCFM. It can be obtained from catalog ratings, or sometimes by calculation if catalog ratings are not available. The method of calculating displacement of a hydraulic pump, given in Design Data Sheet 2 can be adapted to an air pump if measurements can be made.
Tank capacities are shown across the top of the chart. Capacities not shown can be estimated by proportion, since running time is directly proportional to tank capacity. It takes exactly twice as long on a tank twice as large to pump it to the same vacuum.
Vacuum level is shown in the first column in ˝Hg (inches of mercury). Vacuum levels not shown cannot be estimated by proportion since running time is not proportional to the degree of vacuum. The formula given on the back of this sheet can be used for vacuum levels not shown.
Since the chart is calculated for a vacuum pump which has 1 SCFM displacement, chart values must be adjusted for other pumps by dividing them by SCFM displacement of the pump to be used.
Although the chart is for a vacuum pump which will deadhead at 28˝ Hg, the chart is calculated only up to 27˝. Running times for the last few inches up to deadhead vacuum may have considerable error because internal slippage increases and becomes a greater percentage of the air pumped. Vacuum pumps should not be operated too close to their deadhead pressure; they operate inefficiently and tend to overheat.
Running Time Starting with Atmospheric Pressure
Example: Estimate evacuation time of a 300 gallon tank, to a vacuum level of 20˝ Hg, using a vacuum pump having a free running displacement of 9 SCFM.
Solution: From the chart find the running time of 50.1 minutes for a pump having 1 SCFM displacement. Then:
50.1 ÷ 9 = 5.67 minutes for a 9 SCFM pump
Running Time Starting with a Lower Vacuum
Example: Estimate evacuation time to develop a 24˝ Hg vacuum in a 25 cubic foot tank, starting from a vacuum of 12˝ Hg, and using a 6 SCFM vacuum pump.
Solution: This problem must be solved by estimating the time from atmosphere up to a 12˝ vacuum, estimating time from atmosphere up to a 24˝ vacuum, then subtracting the two. The difference will be the desired answer.
Atmosphere to 12˝ Hg: 14.0 minutes per 7 SCFM capac.
Atmosphere to 24˝ Hg: 48.6 minutes per 1 SCFM capac.
48.6 – 14.0 = 34.6 minutes per 1 SCFM capacity.
Adjust for 6 SCFM pump: 34.6 ÷ 6 = 5.77 minutes
Formula for Any Vacuum Pump
This formula, published by Gast, should give a close estimate for any vacuum pump, any size tank, and to any degree of vacuum:
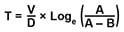
T is pumping time, in minutes.
V is volume of tank, in cubic feet.
D is free running displacement of vacuum pump.
A is deadhead vacuum of pump (with inlet blocked) rating.
B is desired vacuum level in tank, in ˝Hg.
FLOW OF VACUUM THROUGH ORIFICES
Suction cups and vacuum grippers are used for lifting, transferring, or separating many types of sheet materials including paper, sheet metal, cloth, plastic, leather, even concrete slabs.
Suction cups require only a small vacuum pump because the vacuum is essentially “static”, and there is no loss of vacuum after the cup has attached itself to the work. Connecting lines to the cup should be short, and small in diameter, to minimize the air space to be evacuated; so the vacuum pump can build up the vacuum rapidly.
Vacuum gripper pads are used to cover a large area. They have many tiny holes for the vacuum to contact the work. The holes covered by the work are like suction cups; they require very little vacuum pump capacity. But any holes which are not covered by the work waste vacuum and require increased pump capacity. When designing a vacuum gripper, the problem is to select a vacuum pump large enough to provide a “flowing vacuum for the open holes while maintaining sufficient vacuum on the closed holes. This chart will help to estimate the loss of vacuum through the open holes. The application must be carefully specified as to the maximum number of holes which may remain uncovered during operation of the gripper, and their diameter.
The shape of the holes in the gripper will make a difference in the amount of vacuum lost when the hole is open but will not reduce its effectiveness when it is covered. Well rounded orifices result in a maximum loss of vacuum. The holes should be sharp edged to produce maximum turbulence to flow and a minimum loss of vacuum. Knife edge holes will reduce vacuum loss by about 35% over the loss through holes with well rounded edges.
Values of flow in the chart are 2/3rds the flow of perfect orifices with 100% flow coefficient, and should be reasonably close to performance obtained with knife-edged holes.
Example: Find the SCFM vacuum pump capacity to maintain a vacuum of 12˝ Hg through a gripper pad if 8 holes of 1/16˝ diameter remain uncovered.
Solution: The chart shows a consumption of. 725 SCFM per hole or 8 × 0.725 = 5.80 total SCFM. A suitable vacuum pump must be selected by consulting performance graphs published by the pump manufacturer to determine the pump displacement to produce 5.80 SCFM flow at 12˝ Hg.
Orifice Flow Chart
Figures in the body of this chart are SCFM of air flow through sharp edge orifices under the influence of vacuum. A more complete chart will be found in Design Data Sheet 9.
| Vacuum Degree, ˝Hg | Orifice Diameter, Inches | |||||
| 1/64˝ | 1/32˝ | 1/16˝ | 1/8˝ | 1/4˝ | 3/8˝ | |
| 10″ | 0.041 | 0.165 | 0.660 | 2.64 | 10.6 | 23.8 |
| 12″ | 0.045 | 0.180 | 0.725 | 2.89 | 11.6 | 26.0 |
| 14″ | 0.048 | 0.195 | 0.780 | 3.12 | 12.4 | 28.0 |
| 18″ | 0.055 | 0.220 | 0.880 | 3.53 | 14.0 | 31.8 |
| 24″ | 0.063 | 0.250 | 1.00 | 4.04 | 16.2 | 36.4 |
Efficiency of a Vacuum Pump
The efficiency rating of a vacuum pump is said to be the percentage of a perfect vacuum which it will pull against a plugged inlet port. Maximum vacuum ratings are usually stated as the number of inches of mercury (˝Hg) which it will pull when the barometric pressure stands at 30˝ Hg. Therefore, a pump which has a catalog rating of 28˝ Hg maximum is said to have an efficiency of 28 ÷ 30 = 0.93 or 93%. When operating at other barometric pressures it will pull the same percentage of the barometric pressure. For example, in sections of the Rocky Mountains where the barometric pressure may be only 25˝ Hg, the pump can develop only 93% of this: 25 × 0.93 = 23.25˝ Hg. For this reason, vacuum machines which may be installed in various parts of the world are usually designed to perform properly on no more than 20˝ Hg so they can operate in virtually any barometric environment. The maximum vacuum can be limited by installing a vacuum relief valve in the pump inlet line.
© 1990 by Womack Machine Supply Co. This company assumes no liability for errors in data nor in safe and/or satisfactory operation of equipment designed from this information.